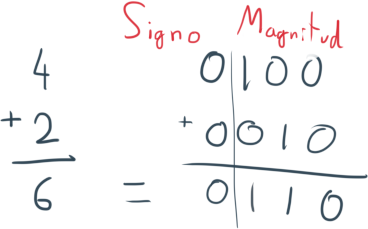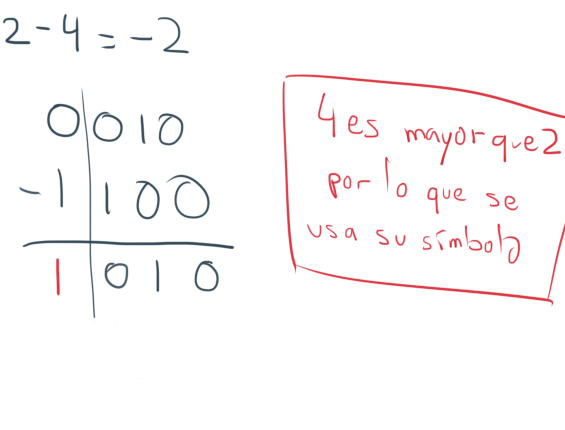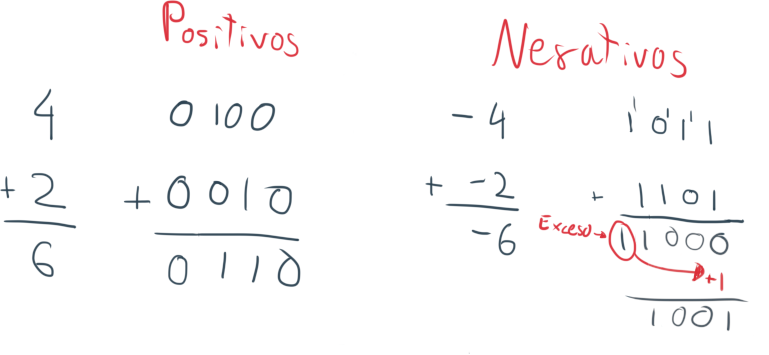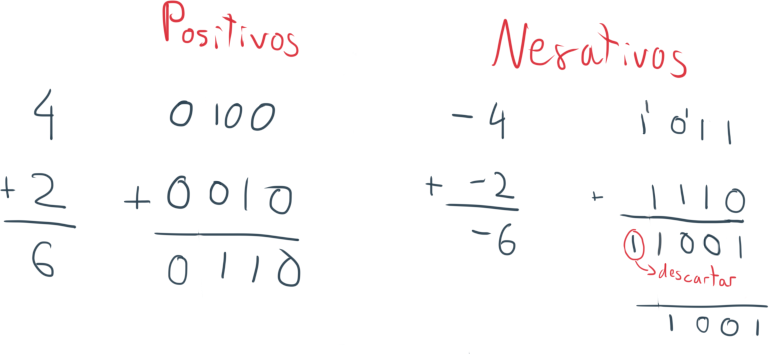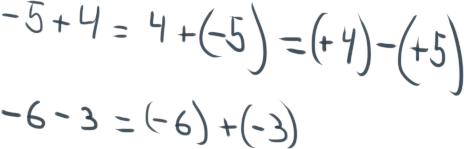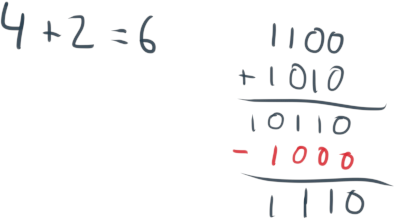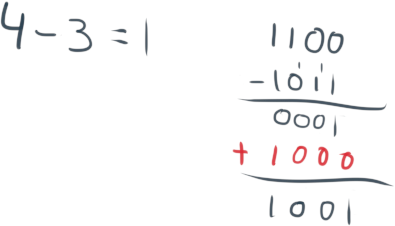Signo y magnitud, complemento a 1 y a 2 y el exceso Z para tontos
La aritmética binaria, al igual que toda rama de las matemáticas, puede ser tediosa, frustrarte y complicada si no se tiene una explicación simple y unas buenas bases. En esta entrada intentaré explicar las operaciones de suma y resta utilizadas por las máquinas de la manera lo más simple que pueda.
Para empezar, debemos comprender que las máquinas funcionan con el sistema binario (del 0 al 1), y no con el decimal (del 0 al 9). Para diferenciarlo y remarcarlo pondremos a veces los números en base 10 (n10) o en base 2 (n2).
Introducción
Antes que nada, debo remarcar que esto se puede realizar con cualquier cantidad de bits, pero en esta entrada solo usaremos 4 bits para mostrar ejemplos más sencillos.
Los bits en binario irán del 0000 al 1111, el valor de estos tendrán un significado diferente en cada ocasión, tendremos tablas para mostrarlo más visualmente.
Signo y Magnitud
El sistema de Signo y Magnitud utiliza el primer bit para identificar si el número es positivo o negativo, 0 indica que el número es positivo y 1 negativo. De esta forma, con un total de 4 bits, podemos obtener desde el 7 hasta el -7. El número 0 también tiene su contraparte negativa.
| Número decimal | Representación Signo y Magnitud |
|---|---|
| 8 | - |
| 7 | 0111 |
| 6 | 0110 |
| 5 | 0101 |
| 4 | 0100 |
| 3 | 0011 |
| 2 | 0010 |
| 1 | 0001 |
| 0 | 0000 |
| -1 | 1001 |
| -2 | 1010 |
| -3 | 1011 |
| -4 | 1100 |
| -5 | 1101 |
| -6 | 1110 |
| -7 | 1111 |
| -8 | - |
Cuando sumar y cuando restar
Es importante saber en qué momento hay que operar con suma y en cual se utiliza la resta. En el caso del Signo y Magnitud se realiza una suma cuando los signos son iguales, y se resta cuando son distintos signos.
Tenemos que tener en cuenta que en -5 - 4 se tendría que realizar una suma, porque el signo - se lo lleva el 4, resultando en -5 + (-4) y ambos dígitos tienen el mismo signo.
Suma
La suma en Signo y Magnitud se realiza como una suma binaria normal y corriente, obviando el primer dígito, que indica el Signo.
En las sumas ambos signos son iguales, por lo que el signo se mantiene, ya sea 1 o 0.
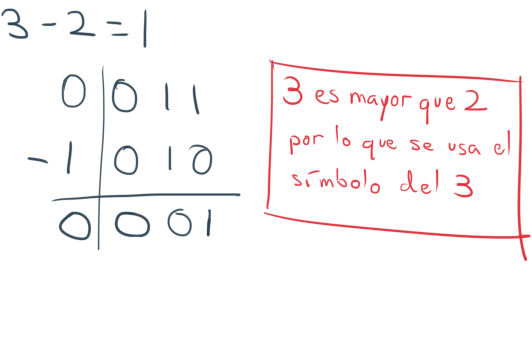
Resta
La resta se hace cuando el signo de ambos números es distinto. Se opera como una resta normal, apartando los símbolos. El símbolo que queda como resultado es el del número de mayor magnitud.
Complemento a 1
La representación del complemento a 1 (a partir de ahora C1) utiliza como base el Signo y Magnitud. El C1 no varía frente al Signo y Magnitud cuando se trata de números positivos. En los números negativos se debe calcular la diferencia entre el número máximo (710 en nuestro caso porque nuestro máximo binario es 1112) y nuestro número. Por ejemplo, el C1 de 6 es 1 porque solo le falta 1 número para llegar a 7, el C1 de 3 es 4 porque le faltan 4 números para llegar a 7.
Una forma rápida de calcular esto en binario es invirtiendo la magnitud de los números negativos. Siempre manteniendo intacto el primer bit, porque este indica el signo. Quedando así el 1100 como 1011. A continuación una tabla comparativa.
| Decimal | Signo y Magnitud | Complemento a 1 |
|---|---|---|
| 8 | - | - |
| 7 | 0111 | 0111 |
| 6 | 0110 | 0110 |
| 5 | 0101 | 0101 |
| 4 | 0100 | 0100 |
| 3 | 0011 | 0011 |
| 2 | 0010 | 0010 |
| 1 | 0001 | 0001 |
| 0 | 0000 | 0000 |
| -0 | 1000 | 1111 |
| -1 | 1001 | 1110 |
| -2 | 1010 | 1101 |
| -3 | 1011 | 1100 |
| -4 | 1100 | 1011 |
| -5 | 1101 | 1010 |
| -6 | 1110 | 1001 |
| -7 | 1111 | 1000 |
| -8 | - | - |
Cuando sumar y cuando restar
La norma de oro es que siempre se suma en los complementos. Cuando se trata de 5 + 2 puede parecer fácil, pero cuando nos encontramos un 5 - 2 debemos juntar el signo - con el número siguiente, quedando así 5 + (-2).
Con los números negativos pasa lo mismo, un -5 - 2 se transforma en -5 + (-2).
Suma
En este caso, a diferencia del Signo y Magnitud, el signo se incluye en la suma.
Habrá ocasiones donde aparezca un exceso. El exceso es aquel número que sobrepasa el límite de nuestras operaciones. En este caso, trabajamos con un máximo de 4 dígitos (de 0000 a 1111), un exceso sería el 10000.
Cuando aparece un exceso, se retira y se suma al resultado. Aquí vemos un ejemplo:
Podemos comprobar en la tabla de arriba como 1001 coincide con -6 en C1.
Complemento a 2
Para conseguir el Complemento a 2 (a partir de ahora C2) se debe obtener primero el C1 y sumarle 1 a los número negativos. El objetivo de esto es evitar la suma del número excedido que se realiza siempre en el C1. Como siempre, aquí vamos con una tabla comparativa.
| Decimal | Signo y Magnitud | Complemento a 1 | Complemento a 2 |
|---|---|---|---|
| 8 | - | - | - |
| 7 | 0111 | 0111 | 0111 |
| 6 | 0110 | 0110 | 0110 |
| 5 | 0101 | 0101 | 0101 |
| 4 | 0100 | 0100 | 0100 |
| 3 | 0011 | 0011 | 0011 |
| 2 | 0010 | 0010 | 0010 |
| 1 | 0001 | 0001 | 0001 |
| 0 | 0000 | 0000 | 000 |
| -0 | 1000 | 1111 | - |
| -1 | 1001 | 1110 | 1111 |
| -2 | 1010 | 1101 | 1110 |
| -3 | 1011 | 1100 | 1101 |
| -4 | 1100 | 1011 | 1100 |
| -5 | 1101 | 1010 | 1011 |
| -6 | 1110 | 1001 | 1010 |
| -7 | 1111 | 1000 | 1001 |
| -8 | - | - | 1000 |
Suma
Con el cambio que ya hemos realizado en la tabla, a partir de ahora la suma se realiza exactamente igual. La única diferencia ahora es que el número excedente se descarta en lugar de sumarlo. Recordamos que los positivos son iguales en el C2, el C1 y el Signo y Magnitud
Exceso Z
El Exceso Z varía dependiendo de la cantidad de dígitos con los que trabajemos, en este caso solo con 4. Para calcular el Exceso Z tenemos que saber que Z = 2(n-1) siendo n el número de dígitos. Z = 2(4-1) = 23 = 8. Con esto conseguimos saber cual es el número máximo que podemos obtener. Como podemos observar en las tablas de arriba, el número 8 y -8 siempre aparecen como primera y última opción.
Ahora que conocemos el número mínimo y máximo, tenemos que tener en cuenta que el mínimo será el 0 a partir de ahora, en otras palabras, -810 = 00002. Para tenerlo de forma más visual y con sentido, vamos a ver la tabla.
| Decimal | Signo y Magnitud | Complemento a 1 | Complemento a 2 | Exceso Z |
|---|---|---|---|---|
| 8 | - | - | - | - |
| 7 | 0111 | 0111 | 0111 | 1111 |
| 6 | 0110 | 0110 | 0110 | 1110 |
| 5 | 0101 | 0101 | 0101 | 1101 |
| 4 | 0100 | 0100 | 0100 | 1100 |
| 3 | 0011 | 0011 | 0011 | 1011 |
| 2 | 0010 | 0010 | 0010 | 1010 |
| 1 | 0001 | 0001 | 0001 | 1001 |
| 0 | 0000 | 0000 | 000 | 1000 |
| -0 | 1000 | 1111 | - | - |
| -1 | 1001 | 1110 | 1111 | 0111 |
| -2 | 1010 | 1101 | 1110 | 0110 |
| -3 | 1011 | 1100 | 1101 | 0101 |
| -4 | 1100 | 1011 | 1100 | 0100 |
| -5 | 1101 | 1010 | 1011 | 0011 |
| -6 | 1110 | 1001 | 1010 | 0010 |
| -7 | 1111 | 1000 | 1001 | 0001 |
| -8 | - | - | 1000 | 0000 |
Si se es observador, se puede ver como el Exceso Z es igual al C2 con el signo invertido. Esta es una forma más fácil de obtenerlo.
Cuando sumar y cuando restar
Ya hemos visto como en Signo y Magnitud se sumaba con los signos iguales y restaba con signos distintos, y en los complementos siempre se suma. En este caso, nuestro objetivo será hacer que ambos números tengan el mismo signo.
Una vez hayamos preparado la operación, será hora de sumar o restar dependiendo de las circunstancias.
Suma
Inicialmente, la suma se realiza de forma normal, teniendo en cuenta el signo durante la operación. Tras sumar, debemos restar el Exceso Z, recordamos que en nuestro caso es 810 = 10002. Siempre va a ser un 1 en la posición más alta, seguido de 0 en el resto de posiciones.
Resta
En el caso de la resta, también haremos la operación de forma normal. Cuando tengamos el resultado, tendremos que sumar el Exceso Z.</p>